Kampfsystem (Civ4): Unterschied zwischen den Versionen

Version vom 28. Juni 2007, 13:51 Uhr

Dieser Artikel wird gerade überarbeitet. Eine aktualisierte Version wird in Kürze zur Verfügung stehen.

Einführung

In diesem Artikel wird das Kampfsystem von Civilisation 4 erläutert. Der Artikel wird Schrittweise auf die einzelnen Berechnungen eingehen. Ziel des Artikels ist dazustellen, wie sich die Wahrscheinlichkeit, mit der eine Einheit eine andere besiegt, berechnen lässt.

In den Nachfolgenden Abschnitten wird Grundsätzliches zum Kampfverlauf geschildert und es wird auf die einen Teil der Notation eingegangen. Immer, wenn neue Begriffe auftauchen, wird gleich die Schreibweise mit benannt. So wird nicht zuviele Symbole auf einmal auf einen einstürmen.

Im 2.Teil werden die ganzen Vorberechnungen erläutert, die für die Hauptberechnungen im 3.Teil unerlässlich sind. Es werden folgende Begriffe eingeführt, erläutert und mit Beispielen untermauert:

• Ist-Gesamtstärke und Soll-Gesamtstärke
• Feuerkraft
• Schaden pro Runde oder der Angriffswert
• Anzahl an Kampfrunden, die eine Einheit verlieren kann, eher sie besiegt ist
• Wahrscheinlichkeit, eine Kampfrunde zu gewinnen bzw. zu verlieren

Im 3.Teil kommen wir zu den eigentlichen Hauptberechnungen. Zentrales Hilfsmittel ist die sogenannte Binominalverteilung. Sie wird kurz umrissen werden. Es wird dann gezeigt, wie sich die Wahrscheinlichkeit, mit der ein Kampf gewonnen wird, berechnen lässt, ohne auf das Konzept der Erstschläge einzugehen. Auch hier wird es wieder eine Beispielrechnung geben. Anschließend wird dann auf das Konzept der Erstschläge eingegangen. Es wird erläutert, was Erstschläge überhaupt sind, was sie bewirken und welchen Einfluss sie auf die Berechnungen der Siegwahrscheinlichkeit ausüben. (Es sei angemerkt, dass sich durch die Erstschläge die Berechnungen "etwas" komplizierter werden, allerdings in einem noch erträglichem Maße.)

Allgemeines

Zuerst soll hier erstmal die genauen Rahmenbedingungen erklärt werden, d.h. wie ein Kampf in Civ4 überhaupt abläuft:

1. An einem Kampf sind genau zwei Einheiten beteiligt: der Angreifer und der Verteidiger.
2. Als Angreifer wird diejenige Einheit angesehen, die selbst ein benachtbartes Feld betritt, in der sich eine andere, feindliche Einheit aufhält, diese wird dann als Verteidiger bezeichnet.
3. Festlegung auf Angreifer und Verteidiger hat nur Einfluss darauf, wer welche Art von Boni bzw. Mali bekommen kann. Der Verteidiger z.B. bekommt immer Boni durch das Gelände (falls vorhanden), in dem er sich zum Zeitpunkt des Angriffs befindet. Der Angreifer bekommt solche Boni nie. Außerdem gibt es noch ein paar Besonderheiten derart, wer welche Art von Boni bzw. Mali bekommt. Darauf wird weiter unten eingegangen.
4. Als Ausgänge eines Kampfes kommen nur ein Sieg des Angreifers oder ein Sieg des Verteidigers in Betracht. Falls der Angreifer den Kampf verliert, kann er sich noch unter gewissen Umständen aus dem Kampf zurückziehen. Auch darauf wird weiter unten eingegangen.
5. Gewinnt eine Einheit einen Kampf (egal ob Angreifer oder Verteidiger), so wird er in den meisten Fällen verletzt aus dem Kampf gehen. Jede Einheit besitzt nach ihrer Errichtung volle 100 Trefferpunkte (Abkürzung Tp). Eine Einheit gilt als vernichtet, wenn sie genau 0 Tp besitzt. Dies tritt nur nach einer Niederlage in einem Kampf auf. Eine Einheit kann sich nach dem Kampf von ihren Verletzungen erholen.
6. Ein Kampf läuft in einzelnen Runden ab (nicht zu verwechseln mit einer normalen Civ4 Runde!). Eine Kampfrunde wird entweder von dem Angreifer gewonnen oder von dem Verteidiger, ein Unentschieden ist nicht möglich. Gewinnt der Angreifer eine Runde, so erhält der Verteidiger einen Treffer, seine Gesundheit verringert sich dem entsprechend dem Angriffswert des Angreifers (mit Angriffswert ist nicht die Stärke gemeint! Siehe weiter unten). Gewinnt der Verteidiger, so gilt entsprechendes für den Angreifer.
7. Ein Kampf gilt genau dann als beendet, wenn entweder der Angreifer oder der Verteidiger nur noch 0 Tp besitzten. Diese Einheit gilt als vernichtet und wird vom Spiel entfernt. Einzige Ausnahme betrifft die bereits angesprochene Rückzugsmöglichkeit des Angreifers. Dieser Fall tritt dann ein, wenn der Angreifer fast erledigt ist und somit ein letzter Treffer des Verteidigers ihn vernichten würde. Würde dann der Verteidiger diese Kampfrunde gewinnen, so zieht sich der Angreifer zurück, ohne den Treffer einzustecken.
8. Eine verringerte Gesundheit hat direkte Auswirkung auf die Stärke einer Einheit. Ist eine Einheit schwer verletzt, ist sie kaum noch kampffähig. Auf diese Weise ist es möglich, eigentlich sehr starke Einheiten wie z.B. einen Panzer mit einer verhältnismäßigen schwachen Einheit (z.B. ein Speerkämpfer) zu besiegen.
9. Die Stärke einer Einheit ändert sich während eines Kampfes nicht, auch nicht, sollte er verletzt werden. Verletzungen machen sich erst beim nächsten Kampf bemerkbar.
10. Boni können die Kampfkraft einer Einheit deutlich erhöhen, durch Mali kann sie aber auch deutlich verringert werden.
11. Eine Einheit kann befördert werden. Die meisten Beförderungen geben Boni auf bestimmte Kampfbedingungen, z.B. gibt die Beförderung Schock einer Einheit einen +25% Bonus gegen Nahkampeinheiten.

Definitionen

Hier werden einige Definitionen aufgeführt, die in den ersten Gleichungen auftauchen. Im fließenden Text werden sie so nie verwendet.

• [math]a[/math] := Angreifer
• [math]v[/math] := Verteidiger

Diese beiden Definitionen tauchen nur als Indizes auf. [math]a[/math] und [math]v[/math] nehmen auch keine Zahlenwerte an, sie dienen nur zur Unterscheinung der anderen Variablen. Die folgenden Definitionen werden ebenfalls nur in Gleichungen verwendet. Alle können unterschiedliche Werte annehmen, abhängig von ihrem Definitionsbereich, der gleich mit angegeben ist. Sie bilden gewissermaßen die Grundlage, da durch sie eine Einheit bestimmt wird. So wird eine Einheit bestimmt durch ihre Stärke, ihre Gesundheit, ihre Boni, ihre Mali und die Anzahl ihrer Erstschläge. Alle anderen Begriffe werden von den Grundbegriffen hier hergeleitet.

Die Grundbegriffe und ihre Definitionen für den Angreifer:

• [math]S_a[/math]:= Sollstärke des Angreifers, wobei [math]S_a \in \mathbb{N}[/math].
• [math]B_a[/math]:= Boni des Angreifers, wobei [math]B_a \in \mathbb{N}_0[/math].
• [math]M_a[/math]:= Mali des Angreifers, wobei [math]M_a \in \mathbb{N}_0[/math].
• [math]G_a[/math]:= Gesundheit des Angreifers, wobei [math] G_a \in [1,100] \subset\mathbb{N}[/math].
• [math]E_a[/math]:= Anzahl der Erstschläge des Angreifers, wobei [math]E_a \in \mathbb{N}_0[/math].

Und hier für den Verteidiger:

• [math]S_v[/math]:= Sollstärke des Verteidigers, wobei [math]S_v \in \mathbb{N}[/math].
• [math]B_v[/math]:= Boni des Verteidigers, wobei [math]B_v \in \mathbb{N}_0[/math].
• [math]M_v[/math]:= Mali des Verteidigers, wobei [math]M_v \in \mathbb{N}_0[/math].
• [math]G_v[/math]:= Gesundheit des Verteidigers, wobei [math] G_a \in [1,100] \subset\mathbb{N}[/math].
• [math]E_v[/math]:= Anzahl der Erstschläge des Verteidigers, wobei [math]E_a \in \mathbb{N}_0[/math].

Anmerkung: [math] \mathbb{N} [/math] steht für die Menge der natürlichen Zahlen ohne die Null, [math] \mathbb{N}_0 [/math] steht für die Menge der natürlichen Zahlen mit der Null, [math] [1,100]\subset\mathbb{N} [/math] bezeichnet das abgeschlossene Intervall von 1 bis 100 mit Einträgen aus den natürlichen Zahlen.

Vorberechnungen

Berechnung von Ist-Gesamtstärke und Soll-Gesamtstärke

Als erstes wird die Istgesamtstärke für den Angreifer und den Verteidiger berechnet (Schreibweise: [math]I_a\,\text{bzw}\,I_v\,)[/math]:

[math] I_a = \left{\begin{array}{cl} S_a\, \left( 1 %2B+ \frac{B_a - M_a}{100} \right)\, \cdot \, \frac{G_a}{100}\,, & \mbox{wenn}\,B_a - M_a \geq 0 \\ S_a \, \left(1 %2B+ \left|\frac{B_a - M_a}{100}\right|\right)^{-1}\, \cdot \, \frac{G_a}{100}\,, & \mbox{wenn}\,B_a - M_a\lt 0 \end{array}\right [/math]

[math] I_v = \left{\begin{array}{cl} S_v\, \left( 1 %2B+ \frac{B_v - M_v}{100} \right)\, \cdot \, \frac{G_v}{100}\,, & \mbox{wenn}\,B_v - M_v \geq 0 \\ S_v \, \left(1 %2B+ \left|\frac{B_v - M_v}{100}\right|\right)^{-1}\, \cdot \, \frac{G_v}{100}\,, & \mbox{wenn}\, B_v - M_v\lt 0 \end{array}\right [/math]

Die Ist-Gesamtstärke hängt von den jeweiligen Boni und Mali ab sowie von der aktuellen Gesundheit. Ist die Differenz von Boni und Mali größer als Null, wird die große Klammer mit der Stärke multipliziert, ist die Differenz kleiner als Null, wird die Stärke durch die große Klammer dividiert.

Anschließend wird die Soll-Gesamtstärke für den Angreifer und den Verteidiger berechnet (Schreibweise: [math] \mathfrak{S}_a\,\text{bzw.}\,\mathfrak{S}_v[/math]):

[math] \mathfrak{S}_a = \left{\begin{array}{cl} S_a\, \left( 1 %2B+ \frac{B_a - M_a}{100} \right)\,, & \mbox{wenn}\,B_a - M_a \geq 0 \\ S_a \, \left(1 %2B+ \left|\frac{B_a - M_a}{100}\right|\right)^{-1}\,, & \mbox{wenn}\,B_a - M_a\lt 0 \end{array}\right [/math]

[math] \mathfrak{S}_v = \left{\begin{array}{cl} S_v\, \left( 1 %2B+ \frac{B_v - M_v}{100} \right)\,, & \mbox{wenn}\,B_v - M_v \geq 0 \\ S_v \, \left(1 %2B+ \left|\frac{B_v - M_v}{100}\right|\right)^{-1}\,, & \mbox{wenn}\, B_v - M_v\lt 0 \end{array}\right [/math]

Die Sollgesamtstärke hängt hier nur von den Boni und Mali ab, nicht aber von der Gesundheit. Ist die Differenz von Boni und Mali größer als Null, wird die große Klammer mit der Stärke multipliziert, ist die Differenz kleiner als Null, wird die Stärke durch die große Klammer dividiert.

Folgendes ist dabei zu beachten:

• Die Beförderungen Kampf I-VI werden grundsätzlich zu dem eigenem Stärkewert addiert.

• Feldjäger I + II, Gebirgsjäger I + II und Stadtverteidigung I-III kommen nur bei Verteidigungseinheiten zum tragen.

• Ausfall, Deckung, Formation, Gebirgsjäger III, Hinterhalt, Schock, Speerfeuer II + III, Stadtangriff I-III und Zangenangriff: Deren Auswirkungen hängen immer von der IST-Stärke des Verteidigers ab.

• Einheitenfähigkeiten (xxx% geg. Einheitentyp/Gelände): Deren Auswirkungen hängen immer von der IST-Stärke des Verteidigers ab.

Beispiel: Schwertkämpfer (A) besitzt Rang I und Bogenschütze (V) Rang II. (Beide bei voller Gesundheit) Gesamtstärke (A) = 6 * 1,10 = 6,60 Gesamtstärke (V) = 3 * 1,20 = 3,60

Beispiel: Ein verletzter Speerkämpfer (V) mit einer IST-Stärke von 2, wird in einem Wald von einem berittenen Bogenschützen (A) mit einer IST-Stärke von 6, und der die Beförderungen Rang I und Schock bezitzt, angegriffen:

Für den Angreifer: IST-Stärke (A) = 6 * 1,10 (+10% Stärke) * 100/100 = 6,60 (Schock wird hier nicht dazu gezählt)

Für den Verteidiger: [Summe aller Boni] - [Summe aller Mali] = 1,5 - 0,25 = 1,25 > 0

Daraus folgt Fall a):

Gesamtstärke (V) = 2 * ( 1 + 0,5 (+50% Waldbonus) + 1,00 (+100% gegen berittene Einheiten) – 0,25 (-25% wegen Schock) = 2 * 2,25 = 4,50

Feuerkraft (Neu ab Patch 1.61)

Als nächstes berechnen wir die Feuerkraft. Sie ist erst seit dem Patch 1.61. für Vanillia dabei und wird ist das arithmetische Mittel aus der Ist-Gesamtstärke und der Soll-Gesamtstärke (Schreibweise: [math]F_a\,\mbox{bzw}\, F_v[/math]):

[math]F_a = floor\left(\frac{I_a %2B+ \mathfrak{S}_a}{2}\right) [/math]

[math]F_v = floor\left(\frac{I_v %2B+ \mathfrak{S}_v}{2}\right) [/math]

Dabei bedeutet hier [math] floor(.) [/math] das Abrunden auf die 2.Nachkommastelle.

Anmerkung: Die Feuerkraft wird im Spiel angezeigt, und zwar dort, wo man auch die Siegeswahrscheinlichkeit eines Kampfes betrachten kann. Daran kann man auch gut erkennen, wie die verschiedenen Boni bzw. Mali wirken können. (Man wird also insbesondere sehen, wenn der Angreifer z.B. +25% gegen den Verteidiger hat, dass nicht die Feuerkraft des Angreifers von dem Bonus profitiert, sondern die Feuerkraft des Verteidigers dadurch sanktioniert wird.)

Beispiel: Für den ber. Bogenschützen ergibt sich eine Feuerkraft von:

(6,60 + 6,60) / 2 = 6,60 (welch Überraschung)

Für den Speerkämpfer:

(4,50 + 9,00) / 2 = 6,75

Schaden pro Runde

Jetzt berechnen wir, wie viel Schaden eine Einheit pro Kampfrunde verursachen kann. Dazu bestimmen wir den Angriffswert des Angreifers und des Verteidigers (Schreibweise: [math]\mathfrak{A}_a \,\mbox{bzw}\,\mathfrak{A}_v[/math]):

[math]\mathfrak{A}_a = floor\left( 20\,\cdot\, \frac{3\,\cdot\,F_a %2B+ F_v}{3\,\cdot\,F_v%2B+F_a}\right) [/math]

[math]\mathfrak{A}_v = floor\left( 20\,\cdot\, \frac{3\,\cdot\,F_v %2B+ F_a}{3\,\cdot\,F_a%2B+F_v}\right) [/math]

Dabei bedeutet [math]floor(.)[/math] das Abrunden auf die nächstkleinere ganze Zahl. Es wird auf Ganze Zahlen abgerundet. Der Angriffswert hängt von der Feuerkraft des Angreifers und der Feuerkraft des Verteidigers ab.

Beispiel: Für den ber. Bogenschützen ergibt sich: Schaden/Runde (A) = 19 TP Für den Speerkämpfer ergibt sich: Schaden/Runde (V) = 20 TP

Benötigte gewonnene (bzw. verlorene) Kampfrunden zum Sieg

Als nächstes kommt die Berechnung der Anzahl an Kampfrunden dran, die eine Einheit maximal überstehen kann, eher sie den Kampf verliert. Dabei ist diese Anzahl stark abhängig von der momentanen Gesundheit der jeweiligen Einheit, ebenso spielt die Angriffskraft eine Rolle (Schreibweise:[math] R_a \,\mbox{bzw}\, R_v [/math]):

[math] R_a = ceil\left(\frac{G_a}{\mathfrak{A}_v}\right) [/math]

[math] R_v = ceil\left(\frac{G_v}{\mathfrak{A}_a}\right) [/math]

Dabei bedeutet [math]ceil(.)[/math] das Aufrunden auf die nächst größere ganze Zahl. Zu beachten ist, dass mit [math]R_a[/math] die Kampfrunde bezeichnet wird, mit der der Angreifer den Kampf insgesamt verliert. Z.B. meint [math]R_a = 6[/math], dass der Angreifer maximal 5 Kampfrunden verlieren kann, aber dennoch noch die Chance besitzt, den Kampf insgesamt zu gewinnen. Mit der 6. verlorenen Kampfrunde ist der Angreifer dann aber besiegt. Analog für den Verteidiger.

Beispiel: Für den ber. Bogenschützen ergibt sich: BT = 3 Für den Speerkämpfer ergibt sich: BT = 5

Die Wahrscheinlichkeit, eine Kampfrunde zu gewinnen

Als letzte Vorberechnung kommt jetzt die Wahrscheinlichkeit, dass der Angreifer bzw. der Verteidiger eine Kampfrunde gewinnt (Schreibweise: [math] p_a \,\mbox{bzw}\, p_v [/math]):

[math] p_a = \frac{I_a}{I_a %2B+ I_v} [/math]

[math] p_v = \frac{I_v}{I_a %2B+ I_v} [/math]

Es gilt [math] p_a %2B+ p_v = 1 [/math].

Mit den Vorberechnungen sind wir jetzt fertig. Für die eigentlichen (schwierigeren) Berechnungen brauchen wir die Werte für die Anzahl an Kampfrunden, bis der Angreifer bzw. der Verteidiger verlieren, sowie die Wahrscheinlichkeit, mit der eine Kampfrunde gewonnen (bzw. verloren) wird.

Berechnung der endgültigen Siegeschance ( ohne Erstschlag)

Allgemeines

Jetzt kommen wir zud den eigentlichen Berechnungen, die die Wahrscheinlichkeit wiedergibt, einen Kampf zu gewinnen. Dazu erstmal ein paar weitere allgemeine Sachen:

1. Ein Kampf hat genau zwei Ausgänge. Entweder siegt der Angreifer oder der Verteidiger.
2. Die siegreich aus dem Kampf kommende Einheit wird eine Restgesundheit übrig haben, die im Bereich zwischen 1 und derjenigen Gesundheit liegt, mit der gekämpft wurde.
3. Für die siegreiche Einheit können folgende Kampfausgänge eintreten:
   1. [math] G_i [/math]
   2. [math] G_i - \mathfrak{A}_j [/math]
   3. [math] G_i - 2\,\cdot\,\mathfrak{A}_j [/math]
   4. [math] \dots [/math]
   5. [math] G_i - (R_i-1)\,\cdot\,\mathfrak{A}_j\,,\quad\mbox{wobei}\, i,j\in\{a,v},\,i\neq j\,.[/math] Dies bedeutet, [math] i [/math] und [math]j[/math] können für den Angreifer oder den Verteidiger stehen, wobei sie voneinander verschieden sind. (Kleines Beispiel: Angenommen, ein Angreifer mit voller Gesundheit gewinne einen Kampf und der Verteidiger habe einen Angriffswert [math]\mathfrak{A}_v = 17 [/math]. Dann kommen für den Angreifer folgende Kampfausgänge in betracht:
      1. 100 Gesundheit
      2. 83 Gesundheit
      3. 66 Gesundheit
      4. 49 Gesundheit
      5. 32 Gesundheit
      6. 15 Gesundheit
      7. 0 oder weniger Gesundheit ist nicht möglich, andernfalls wäre der Angreifer besiegt, was aber der Voraussetzung, dass er den Kampf gewonnen hat, widerspricht.)
4. Die in 3. eintretenden Kampfausgänge besitzen unterschiedliche Wahrscheinlichkeiten, aus denen sich dann hinterher die Siegeswahrscheinlichkeit zusammensetzt.
5. Diese Wahrscheinlichkeiten werden durch die sogenannte Binominalverteilung ermittelt.

Die Binominalverteilung

Betrachten wir dazu das Modell des fortgesetzten Münzwurf.

Eine Münze wird 5-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass 3-mal die Zahl fällt?

Den 5-maligen Wurf der Münze können wir als eine Null-Eins-Folge interpretieren, wobei die Eins für das Ereignis steht, dass die Zahl fällt, die Null steht dann entsprechend für das Ereignis, dass Kopf fällt. Eine mögliche günstige Kette wäre dann z.B. 1-0-1-1-0.

Die Reihenfolge der Ereignisse ist egal, wichtig ist nur, wieoft die Eins oder die Null kommt.

Die Wahrscheinlichkeit, mit der aus dem 5-maligen Werfen 3-mal die Eins kommt, beträgt [math]{5\choose 3}\,\cdot\, 0.5^3\,\cdot\,0.5^2 = 0.31250 [/math], wobei [math]{5\choose 3} = \frac{5!}{3!\,(5-3)!}[/math] der Binominalkoeffizient ist.

Sei n die Länge einer Null-Eins-Folge. Die Wahrscheinlichkeit, mit der die Folge k-Einsen enthält, beträgt

[math]B(n,p,k)= {n\choose k}\,\cdot\,p^k\,\cdot\,(1-p)^{n-k} [/math], wobei p die Wahrscheinlichkeit dafür ist, mit der eine Eins fällt.

B(n,p,k) bezeichnet man dann als Binominalverteilung.

Formel für die Berechnung der Siegeswahrscheinlichkeit

Betrachten wir einen Kampf, bei dem der Angreifer gewinnt. Wie weiter oben beschrieben, können mehrere Ausgänge eintreten, was den Grad der Verletzung des Angreifers betrifft. Im Folgenden betrachten wir uns den Ausgang, dass der Angreifer unverletzt aus dem Kampf hervor geht. Das bedeutet, der Angreifer darf keine Kampfrunden verlieren, andernfalls würde er verletzt werden, was wir aber erstmal ausschließen.

Führen wir erstmal folgende Definition ein:

Definition Seien [math]R_a[/math] und [math]R_v[/math] die Kampfrunden gemeint, in der der Angreifer bzw. der Verteidiger den Kampf verlieren. Die maximale Anzahl an Kampfrunden ergibt sich dann wie folgt:

[math] R_{max} = R_a %2B+ R_v - 1 [/math]

(-1 deswegen, weil Angreifer und Verteidiger beide gleichzeitig den Kampf nicht verlieren können.)

Als Null-Eins-Folge interpretiert gilt: 1-1-1-...-1 , wobei die Eins dafür steht, dass der Angreifer die Kampfrunde gewinnt. Die Anzahl der Einser ist im diesem Falle gleich den Wert von [math]R_v[/math]. Die Binominalverteilung darauf angewandt ergibt:

[math]B(R_v,p_a,R_v)= {R_v\choose R_v}\,\cdot\,{p_a}^{R_v}\,\cdot\,{p_v}^{R_v-R_v} = {p_a}^{R_v} [/math]

Dies ist die Wahrscheinlichkeit dafür, dass der Angreifer unverletzt den Kampf gewinnt.

Wird der Angreifer einmal getroffen, also er verliert genau eine Kampfrunde, dann gilt:

[math]B(R_v,p_a,R_v-1)\,\cdot\,p_a = {R_v\choose R_v-1}\,\cdot\,{p_a}^{R_v-1}\,\cdot\,p_a\,\cdot\,{p_v}^{R_v-(R_v-1)} = {R_v\choose R_v-1}\,\cdot\,{p_a}^{R_v}\,\cdot\,{p_v}[/math]

Warum [math] B(R_v,p,R_v-1)\,\cdot\,p [/math] und nicht [math] B(R_v%2B+1,p_a,R_v)[/math] ? Hierzu betrachten wir uns die dazu gehörende Null-Eins-Folge: 1-1-...-0-...-1-1 . Die Folge enthält genau eine Null. Diese kann an einer beliebigen Stelle aufhalten, außer an der letzten. Die letzte Eins steht dafür, dass der Angreifer den letzten Treffer gegen den Verteidiger landet und ihn somit besiegt. Würde aber am Ende die einzige Null stehen, würde dass heißen, dass der Kampf nicht zu Ende wäre. Somit muss die letzte Stelle von einer Eins belegt sein. Als Konsequenz reduzieren sich automatisch die möglichen günstigen Anordnungen der Null-Eins-Folge. (Zusammengefasst muss der letzte Treffer immer vom Angreifer kommen, wenn er siegen will.)

Wird der Angreifer zweimal getroffen, so gilt entsprechend:

[math]B(R_v%2B+1,p_a,R_v-1)\,\cdot\,p_a = {R_v%2B+1\choose R_v-1}\,\cdot\,{p_a}^{R_v-1}\,\cdot\,p_a\,\cdot\,{p_v}^{R_v%2B+1-(R_v-1)} = {R_v%2B+1\choose R_v-1}\,\cdot\,{p_a}^{R_v}\,\cdot\,{p_v}^2 [/math]

Allgemein gilt nun für die Wahrscheinlichkeit, dass der Angreifer den Kampf gewinnt:

[math]B(R_v,p_a,R_v) + \sum_{n=R_v}^{R_{max}-1} B(n,p_a,R_v)\,\cdot\,p_a [/math]

Der erste Summand ist gerade die Wahrscheinlichkeit, dass der Angreifer unverletzt den Kampf gewinnt, er also keine Kampfrunde verliert. Der zweite Summand steht dafür, dass der Angreifer genau eine Kampfunde verliert. Der letzte Summand steht dafür, dass der Angreifer [math](R_a - 1)[/math] Kampfrunden verliert, das bedeutet, dass er fast am Ende ist, eine weitere verlorene Runde würde einen Niederlage bedeuten. ([math]R_a - 1[/math] taucht nicht direkt in der Formel auf, es steht aber für die Anzahl aller Summanden.)

Definition:

Seien mit [math]R_a\,,\,R_v\,\in\mathbb{N}[/math] die Runde gemeint, mit der der Angreifer bzw. der Verteidiger den Kampf verliert und seien [math]p_a\,,\,p_v\,\in\,[0,1][/math] die Wahrscheinlichkeiten dafür, dass der Angreifer bzw. der Verteidiger den Kampf gewinnen, [math]p_a %2B+ p_v = 1[/math]. Dann gilt

• [math] P_a:= B(R_v,p_a,R_v) + \sum_{n=R_v}^{R_{max}-1} B(n,p_a,R_v)\,\cdot\,p_a [/math] und
• [math] P_v:= B(R_a,p_v,R_a) + \sum_{n=R_a}^{R_{max}-1} B(n,p_v,R_a)\,\cdot\,p_v [/math],

wobei [math]P_a[/math] für die Siegeswahrscheinlichkeit des Angreifers steht, den Kampf zu gewinnen, [math]P_v[/math] steht entsprechend für die Wahrscheinlichkeit eines Sieges des Verteidigers.

Berechnung der endgültigen Siegeschance ( mit Erstschlag)

Erstschläge

Was sind Erstschläge? Erschläge sind im Prinzip Freirunden, in denen eine Einheit angreifen kann, ohne im Falle einer Niederlage befürchten zu müssen, verletzt zu werden. Erstschläge laufen vor dem eigentlichen Kampf ab. Theoretisch könnte bei einer ausreichend hohen Anzahl an verfügbaren Erstschlägen der Kampf gewonnen werden, ohne dass der Feind die Möglichkeit zur Gegenwehr hätte.

Während eines Kampfes kann entweder nur eine Einheit über Erstschläge verfügen oder überhaupt keine. Beide gleichzeitig ist unmöglich. Wenn also der Angreifer A x-Erstschläge und der Verteidiger V y-Erstschläge verfügen, so gibt die Differenz x-y = e darüber Aufschluss, welcher Fall eintritt:

1) Für e > 0 --> A verfügt über Erstschläge 2) Für e < 0 --> V verfügt über Erstschläge 3) Für e = 0 --> Weder A noch V verfügen über Erstschläge

Verschiedene Einheiten besitzen schon von Natur aus eine bestimmte Anzahl an verfügbaren Erstschlägen. Durch die Erstschlags-Beförderungen (wie sie seit Warlords heißen) kann die Anzahl erhöht werden. Erstschlag I + III bilden eine Ausnahme, sie erhöhen nur die Chance, Erstschläge zur Verfügung zu bekommen. Z.B. gibt Erstschlag I 0-1 Erstschläge.

Wichtig: Die Wahrscheinlichkeit, einen Erstschlag zu erhalten, ist p = 50%.

Endgültige Berechnung

Beispiel: Bogenschütze (V) Schwertkämpfer (A)

(V) : - Boni: +50% Waldbonus / +10% durch Rang I - SOLL-Stärke 3 - SOLL-Gesamtstärke 4,8 - IST-Stärke 2,5 - IST-Gesamtstärke 4 - 2 Erstschläge

(A) : - keine Boni - SOLL-Stärke = IST-Stärke = SOLL-Gesamtstärke = IST-Gesamtstärke = 6

Zitat: Zitat von Tzu Iop Also um das Ganze zu berrechnen brauchen wir auf jeden Fall die Binominalverteilung.

Also was wissen wir über die Szenarios in denen der Bogi gewinnt: 1. Das letzte Ereignis muss ein Treffer des Bogis sein. 2. Der Bogi muss 7mal getroffen haben, um den Schwerti zu besiegen. 3. Der Kampf endet nach dem 7. Treffer des Bogis.

Damit haben wir alle wichtigen Infos. Außerdem vereinfachen wir die Sache erstmal, wir gehen davon aus das der Bogi _keine_ Erstschläge hat.

p = 0,4

a) Bogi gewinnt 7 von 7 Runden, sprich er trifft immer, der Schwerti nie.

B (7; 0,4; 7) = 0,0016...

b) Bogi gewinnt 7 von 8 Runden.

B (7; 0,4; 6) * 0,4 = 0,0069...

Die meisten denken jetzt warum so und nicht B (8; 0,4; 7). Ganz einfach das letzte Ereignis muss ja ein Treffer des Bogis sein. Deshalb sind nur die Ereignisse davor in der Reihenfolge variabel. Wenn man B (8; 0,4; 7) berrechnen würde, würde man auch die Möglichkeit berrechnen, dass der Schwerti in Runde 8 den Bogi verletzt. Diese Möglichkeit exestiert jedoch nicht, da davor bereits 7 Treffer vom Bogi stehen und damit der Kampf schon zu Ende sein muss.

c) 7 von 9 Runden

B (8; 0,4; 6) * 0,4 = 0,01652...

d) 7 von 10 Runden

B (9; 0,4; 6) * 0,4 = 0,02973...

e) 7 von 11 Runden

B (10; 0,4; 6) * 0,4 = 0,04459...

Also Gesamtchance ist dann: 0,0016 + 0,0069 + 0,01652 + 0,02973 + 0,04459 = 0,09934 = 9,934%

Das war jetzt ohne Erstschläge das ganze jetzt nochmal mit. 0 Erstschlagserfolg ist ja identisch mit keine Erstschläge; wird also nicht nochmal berechnet.

1 Erstschlagserfolg:

B(6; 0,4; 6) = 0,0040 B(6; 0,4; 5) * 0,4 = 0,0147 B(7; 0,4; 5) * 0,4 = 0,0310 B(8; 0,4; 5) * 0,4 = 0,0495 B(9; 0,4; 5) * 0,4 = 0,0669

Summe: 16,61%

2 Erstschlagserfolge:

B(5; 0,4; 5) = 0,0102 B(5; 0,4; 4) * 0,4 = 0,0307 B(6; 0,4; 4) * 0,4 = 0,0553 B(7; 0,4; 4) * 0,4 = 0,0774 B(8; 0,4; 4) * 0,4 = 0,0929

Summe: 26,65%

Endgültig für 4 mit 2 Firststrike gegen 6: 9,934% * 0,36 + 16,61% * 0,48 + 26,65% * 0,16 = 15,83%

Das sollte jetzt endgültig richtig sein, es sei denn ich habe mich irgendwo verrechnet. Und hier die Wahrscheinlichkeit, dass der Schwertkämpfer gewinnt.

Zitat: Zitat von Tzu Iop Gleiche Regeln. P = 0,6

0 Erstschläge:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393 B (9; 0,6; 4) * 0,6 = 0,1003 B (10; 0,6; 4) * 0,6 = 0,0669

Summe: 0,9006 = 90,06%

1 Erstschlag:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393 B (9; 0,6; 4) * 0,6 = 0,1003

Summe: 0,8337 = 83,37%

2 Erstschläge:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393

Summe: 0,7334 = 73,34%

Endwahrscheinlichkeit: 90,06% * 0,36 + 83,37% * 0,48 + 73,34% * 0,16 = 84,17%

9,934% + 90,06% = 99,994% 16,61% + 83,37% = 99,98% 26,65% + 73,34% = 99,99%

15,83% + 84,17% = 100,00%

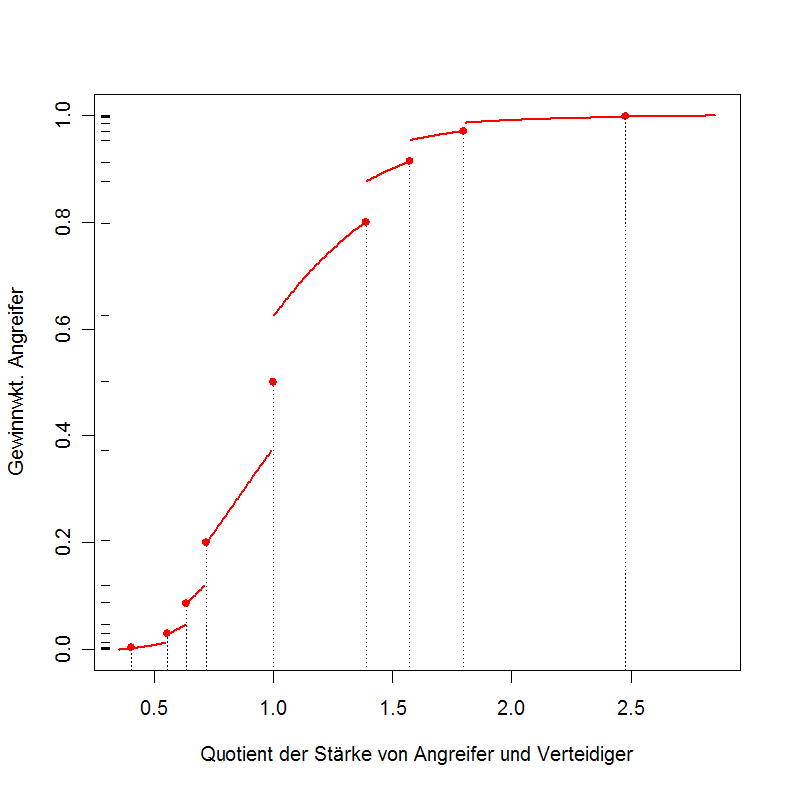
Das Prinzip der "Sprünge"

Man betrachte einen Kampf zwischen zwei gleichstarken Einheiten ( (A) und (V) ). Es sollen folgende Situationen betrachtet werden:

1. (A) erhält keine Rang-Beförderung 2. (A) erhält Rang I 3. (A) erhält Rang II 4. (A) erhält Rang III 5. (A) erhält Rang IV 6. (A) erhält Rang V 7. (A) erhält Rang I und +25% gegen Einheitentyp 8. (A) erhält Rang II und +25% gegen Einheitentyp

Die dazu gehörigen Siegwahrscheinlichkeiten P(E) von (A) sind:

P(1) = 50,00% P(2) = 68,01% P(3) = 72,87% P(4) = 76,98% P(5) = 87,88% P(6) = 90,06%

P(7) = 79,64% P(8) = 90,06%

P(4) = P(7) ( ungefähr) P(6) = P(8)

Bei P(2) (Rang I) und bei P(5) (Rang IV) kommt es zu "Sprüngen". Dazu kommt es, weil sich sich die [Benötigten Treffer zum Sieg] des Verteidigers erhöhen.